Analyzing proportions with the Arrington et al. 2002 example
Source:vignettes/D-ArringtonExample.Rmd
D-ArringtonExample.RmdDISCLAIMER: This example is not terrific because there are empty cells. If you know of a better example of proportions with three factors, do not hesitate to let me know.
Arrington, Winemiller, Loftus, & Akin (2002) published a data set available from the web. It presents species of fish and what proportion of them were empty stomached when caugth. The dataset contained 36000+ catches, which where identified by their Location (Africa, North America, rest of America), by their Trophism (their diet, Detrivore, Invertivore, Omnivore, Piscivore) and by the moment of feeding (Diel: Diurnal or Nocturnal).
The compiled scores can be consulted with
## Location Trophism Diel s n
## 1 Africa Detritivore Diurnal 16 217
## 2 Africa Invertivore Diurnal 76 498
## 3 Africa Invertivore Nocturnal 55 430
## 4 Africa Omnivore Diurnal 2 87
## 5 Africa Piscivore Diurnal 673 989
## 6 Africa Piscivore Nocturnal 221 525
## 7 Central/South America Detritivore Diurnal 68 1589
## 8 Central/South America Detritivore Nocturnal 9 318
## 9 Central/South America Invertivore Diurnal 706 7452
## 10 Central/South America Invertivore Nocturnal 486 2101
## 11 Central/South America Omnivore Diurnal 293 6496
## 12 Central/South America Omnivore Nocturnal 82 203
## 13 Central/South America Piscivore Diurnal 1275 5226
## 14 Central/South America Piscivore Nocturnal 109 824
## 15 North America Detritivore Diurnal 142 1741
## 16 North America Invertivore Diurnal 525 3368
## 17 North America Invertivore Nocturnal 231 1539
## 18 North America Omnivore Diurnal 210 1843
## 19 North America Omnivore Nocturnal 7 38
## 20 North America Piscivore Diurnal 536 1289
## 21 North America Piscivore Nocturnal 19 102One first difficulty with this dataset is that some of the cells are missing (e.g., African fish that are Detrivore during the night). As is the case for other sorts of analyses (e.g., ANOVAs), data with missing cells cannot be analyzed because the error terms cannot be computed.
One solution adopted by Warton & Hui (2011) was to impute the missing value. We are not aware if this is an adequate solution, and if so, what imputation would be acceptable. Consider the following with adequate care.
Warton imputed the missing cells with a very small proportion. In ANOPA, both the proportions and the group sizes are required. We implemented a procedure that impute a count of 0.05 (fractional counts are not possible from observations, but are not forbidden in ANOPA) obtained from a single observation.
Consult the default option with
getOption("ANOPA.zeros")## [1] 0.05 1.00The analysis is obtained with
w <- anopa( {s; n} ~ Trophism * Location * Diel, ArringtonEtAl2002)## ANOPA::fyi(1): Combination of cells missing. Adding:## Trophism Location Diel s n
## Detritivore Africa Nocturnal 0 0
## Detritivore North America Nocturnal 0 0
## Omnivore Africa Nocturnal 0 0## Warning: ANOPA::warning(1): Some cells have zero over zero data. Imputing...The fyi message lets you know that cells are missing;
the Warning message lets you know that these cells were
imputed (you can suppress messages with
options("ANOPA.feedback"="none").
To see the result, use summary(w) (which shows the
corrected and uncorrected statistics) or uncorrected(w) (as
the sample is quite large, the correction will be immaterial…),
uncorrected(w)## MS df F pvalue
## Trophism 0.095656 3 3.351781 0.018102
## Location 0.027449 2 0.961802 0.382203
## Diel 0.029715 1 1.041227 0.307536
## Trophism:Location 0.029485 6 1.033146 0.401285
## Trophism:Diel 0.073769 3 2.584868 0.051365
## Location:Diel 0.005277 2 0.184900 0.831187
## Trophism:Location:Diel 0.011297 6 0.395837 0.882184
## Error(between) 0.028539 InfThese suggests an interaction Diel : Trophism close to significant.
You can easily make a plot with all the 2 x 3 x 4 cells of the design using
anopaPlot(w)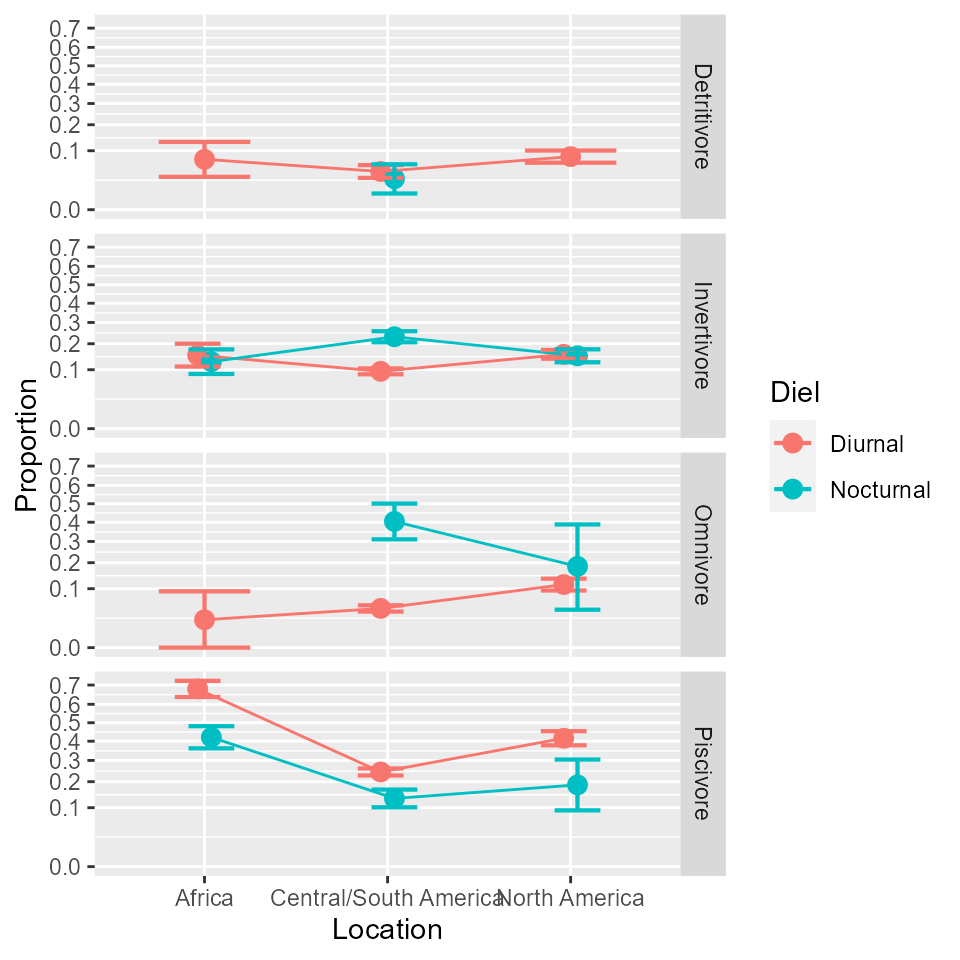
Figure 1. The proportions in the Arrington et al. 2002 data. Error bars show difference-adjusted 95% confidence intervals.
To highlight the interaction, restrict the plot to
anopaPlot(w, ~ Trophism * Location)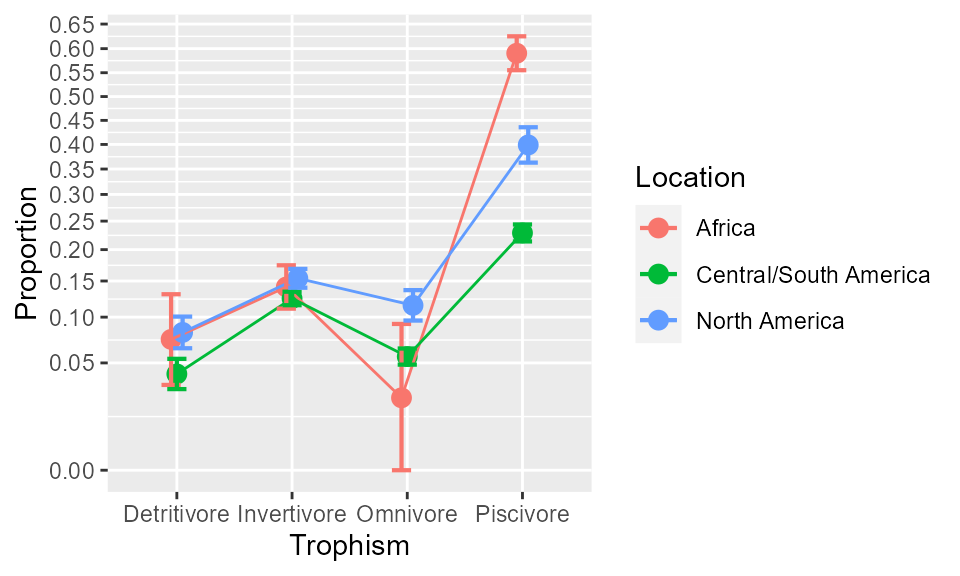
Figure 1. The proportions as a function of class and Difficulty. Error bars show difference-adjusted 95% confidence intervals.
which shows clearly massive difference between Trophism, and small differences between Omnivorous and Piscivorous fishes with regards to Location.
This can be confirmed by examining simple effects (a.k.a. expected marginal analyzes):
e <- emProportions( w, ~ Location * Trophism | Diel )
uncorrected(e)## MS df F pvalue
## Trophism | Diel = Diurnal 0.154120 3 5.400358 0.001031
## Location | Diel = Diurnal 0.023357 2 0.818413 0.441131
## Trophism:Location | Diel = Diurnal 0.013958 6 0.489075 0.817028
## Trophism | Diel = Nocturnal 0.015305 3 0.536291 0.657380
## Location | Diel = Nocturnal 0.009369 2 0.328290 0.720154
## Trophism:Location | Diel = Nocturnal 0.026824 6 0.939909 0.464764As seen, we get a table with effects for each levels of Diel.
For the Diurnal fishes, there is a strong effect of Trophism. However, there is no detectable effect of Location. Finally, there is no interaction.
For the Nocturnal fishes, nothing is significant.
These results don’t quite match the proportions illustrated in the simple effect plot below. The reason is that the simple effect analyses uses a pooled measure of error (the Mean squared error). Sadly, this pooled measured incorporate cells for which the imputations gave tiny sample sizes (n=1). The presence of these three empty cells are very detrimental to the analyses, because if we except these cells, the sample is astonishinly large.
The missing cells are merged with regular cells in the simple effect plots.
library(ggplot2) # for ylab(), annotate()
library(ggh4x) # for at_panel()
library(gridExtra) # for grid.arrange()
#Add annotations to show where missing cells are...
annotationsA <- list(
annotate("segment", linewidth=1.25, x = 1.5, y = 0.45, xend = 1, yend = 0.15, color="green", arrow = arrow()),
annotate("segment", linewidth=1.25, x = 1.5, y = 0.45, xend = 1, yend = 0.10, color="red", arrow = arrow()),
annotate("segment", linewidth=1.25, x = 1.5, y = 0.45, xend = 2.8, yend = 0.25, color="red", arrow = arrow()),
annotate("text", x = 1.5, y = 0.5, label = "No observations")
)
annotationsB <- list(
annotate("segment", linewidth=2, x = 2.2, y = 0.08, xend = 1.95, yend = 0.04, color="red", arrow = arrow()),
annotate("segment", linewidth=2, x = 2.2, y = 0.12, xend = 2.05, yend = 0.36, color="blue", arrow = arrow()),
annotate("text", x = 2.0, y = 0.1, label = "Merge an imputed cell\nwith a regular cell")
)
annotationsC <- list(
annotate("segment", linewidth=2, x = 1.4, y = 0.275, xend = 1.9, yend = 0.285, color="red", arrow = arrow()),
annotate("segment", linewidth=2, x = 1.4, y = 0.275, xend = 2.0, yend = 0.16, color="blue", arrow = arrow()),
annotate("text", x = 1., y = 0.275, label = "Merge an imputed cell\nwith a regular cell")
)
pla <- anopaPlot(w, ~ Trophism * Location * Diel)+
ylab("Proportion empty stomach") +
lapply(annotationsA, \(ann) {at_panel(ann, Diel == "Nocturnal")})
plb <- anopaPlot(w, ~ Diel * Trophism ) +
ylab("Proportion empty stomach") +
annotationsB
plc <- anopaPlot(w, ~ Diel * Location ) +
ylab("Proportion empty stomach") +
annotationsC
grid.arrange( pla, plb, plc, ncol = 3 )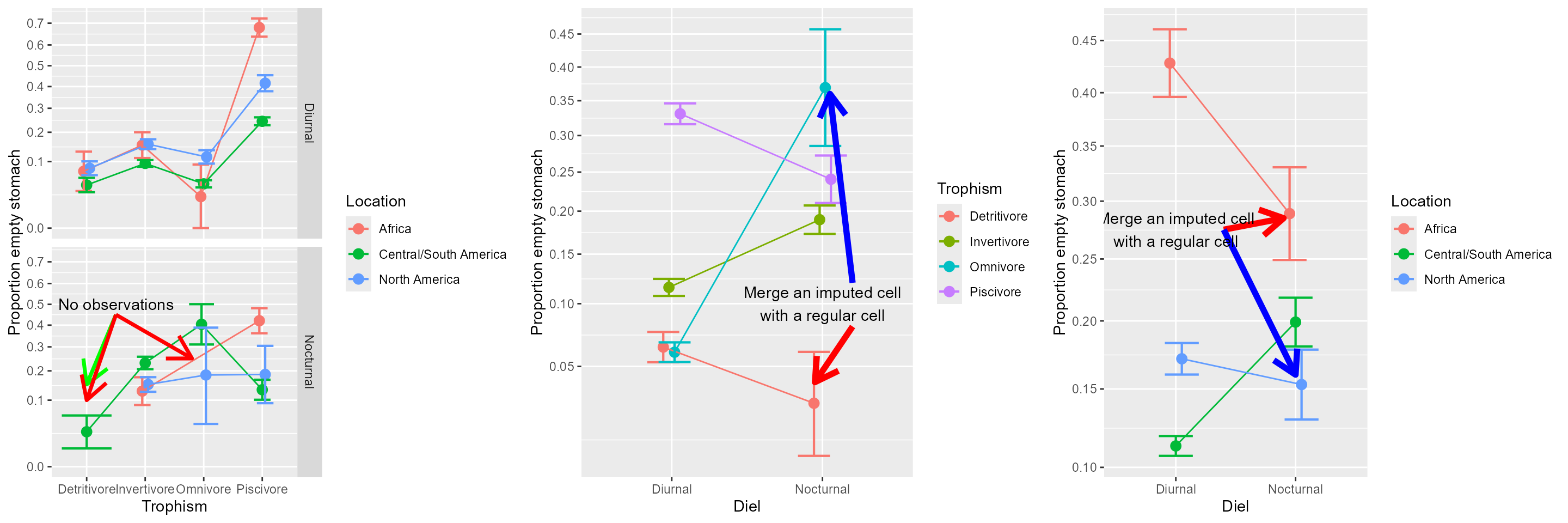
Figure 2. The proportions with arrows highlighting the missing data
Suppose we wish to impute the missing cells with the harmonic mean
number of success (21.6) and the harmonic mean number of observations
per cell (286.9), we could use from the package psych
library(psych)
options("ANOPA.zeros" = c(harmonic.mean(ArringtonEtAl2002$s), harmonic.mean(ArringtonEtAl2002$n)))prior to running the above analyses. In which case it is found that all the effects are massively significant, another way to see that the sample size is huge (over 36,000 fishes measured).