The function GRD() generates a data frame containing
random data suitable for analyses.
The data can be from within-subject or between-group designs.
Within-subject designs are in wide format. The function was originally
presented in Calderini and Harding (2019)
.
GRD(
RenameDV = "DV",
SubjectsPerGroup = 100,
BSFactors = "",
WSFactors = "",
Effects = list(),
Population = list(mean = 0, stddev = 1, rho = 0, scores =
"rnorm(1, mean = GM, sd = STDDEV)"),
Contaminant = list(mean = 0, stddev = 1, rho = 0, scores =
"rnorm(1, mean = CGM, sd = CSTDDEV)", proportion = 0),
Instrument = list(precision = 10^(-8))
)Arguments
- RenameDV
provide a name for the dependent variable (default DV)
- SubjectsPerGroup
indicates the number of simulated scores per group (default 100 in each group)
- BSFactors
a string indicating the between-subject factor(s) with, between parenthesis, the number of levels or the list of level names. Multiple factors are separated with a colon ":" or enumerated in a vector of strings.
- WSFactors
a string indicating the within-subject factor(s) in the same format as the between-subject factors
- Effects
a list detailing the effects to apply to the data. The effects can be given with a list of
"factorname" = effect_specificationor"factorname1*factorname2" = effect_specificationpairs, in which effect_specification can either beslope(),extent(),custom()andRexpression(). For slope and extent, provide a range, for custom, indicate the deviation from the grand mean for each cell, finally, for Rexpression, give between quote any R commands which returns the deviation from the grand mean, using the factors. See the last example below.- Population
a list providing the population characteristics (default is a normal distribution with a mean of 0 and standard deviation of 1)
- Contaminant
a list providing the contaminant characteristics and the proportion of contaminant (default 0)
- Instrument
a list providing some characteristics of the measurement instrument (at this time, its precision only)
Value
a data.frame with the simulated scores.
Note
Note that the range effect specification has been renamed
extent to avoid masking the base function base::range.
References
Calderini M, Harding B (2019). “GRD for R: An intuitive tool for generating random data in R.” The Quantitative Methods for Psychology, 15(1), 1--11. doi:10.20982/tqmp.15.1.p001 .
Examples
# Simplest example using all the default arguments:
dta <- GRD()
head(dta)
#> id DV
#> 1 1 -0.3942900
#> 2 2 -0.0593134
#> 3 3 1.1000254
#> 4 4 0.7631757
#> 5 5 -0.1645236
#> 6 6 -0.2533617
hist(dta$DV)
# Renaming the dependant variable and setting the group size:
dta <- GRD( RenameDV = "score", SubjectsPerGroup = 200 )
hist(dta$score )
# Examples for a between-subject design and for a within-subject design:
dta <- GRD( BSFactors = '3', SubjectsPerGroup = 20)
dta <- GRD( WSFactors = "Moment (2)", SubjectsPerGroup = 20)
# A complex, 3 x 2 x (2) mixed design with a variable amount of participants in the 6 groups:
dta <- GRD(BSFactors = "difficulty(3) : gender (2)",
WSFactors="day(2)",
SubjectsPerGroup=c(20,24,12,13,28,29)
)
# Defining population characteristics :
dta <- GRD(
RenameDV = "IQ",
SubjectsPerGroup = 20,
Population=list(
mean=100, # will set GM to 100
stddev=15 # will set STDDEV to 15
)
)
hist(dta$IQ)
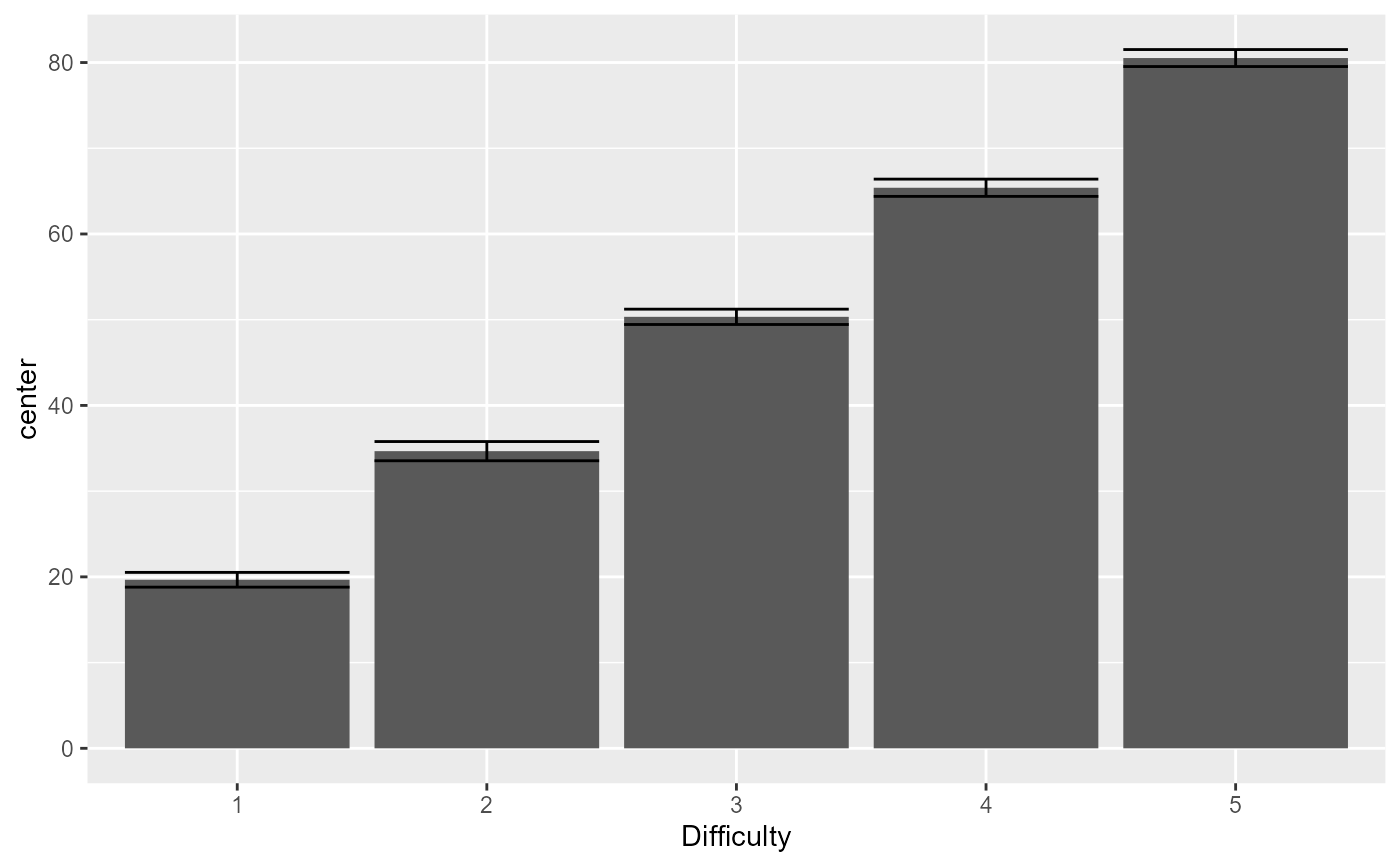
# This example adds an effect along the "Difficulty" factor with a slope of 15
dta <- GRD(BSFactors="Difficulty(5)", SubjectsPerGroup = 100,
Population=list(mean=50,stddev=5),
Effects = list("Difficulty" = slope(15) ) )
# show the mean performance as a function of difficulty:
superb(DV ~ Difficulty, dta )
# An example in which the moments are correlated
dta <- GRD( BSFactors = "Difficulty(2)",WSFactors = "Moment (2)",
SubjectsPerGroup = 250,
Effects = list("Difficulty" = slope(3), "Moment" = slope(1) ),
Population=list(mean=50,stddev=20,rho=0.85)
)
# the mean plot on the raw data...
superb(cbind(DV.1,DV.2) ~ Difficulty, dta, WSFactors = "Moment(2)",
plotLayout="line",
adjustments = list (purpose="difference") )
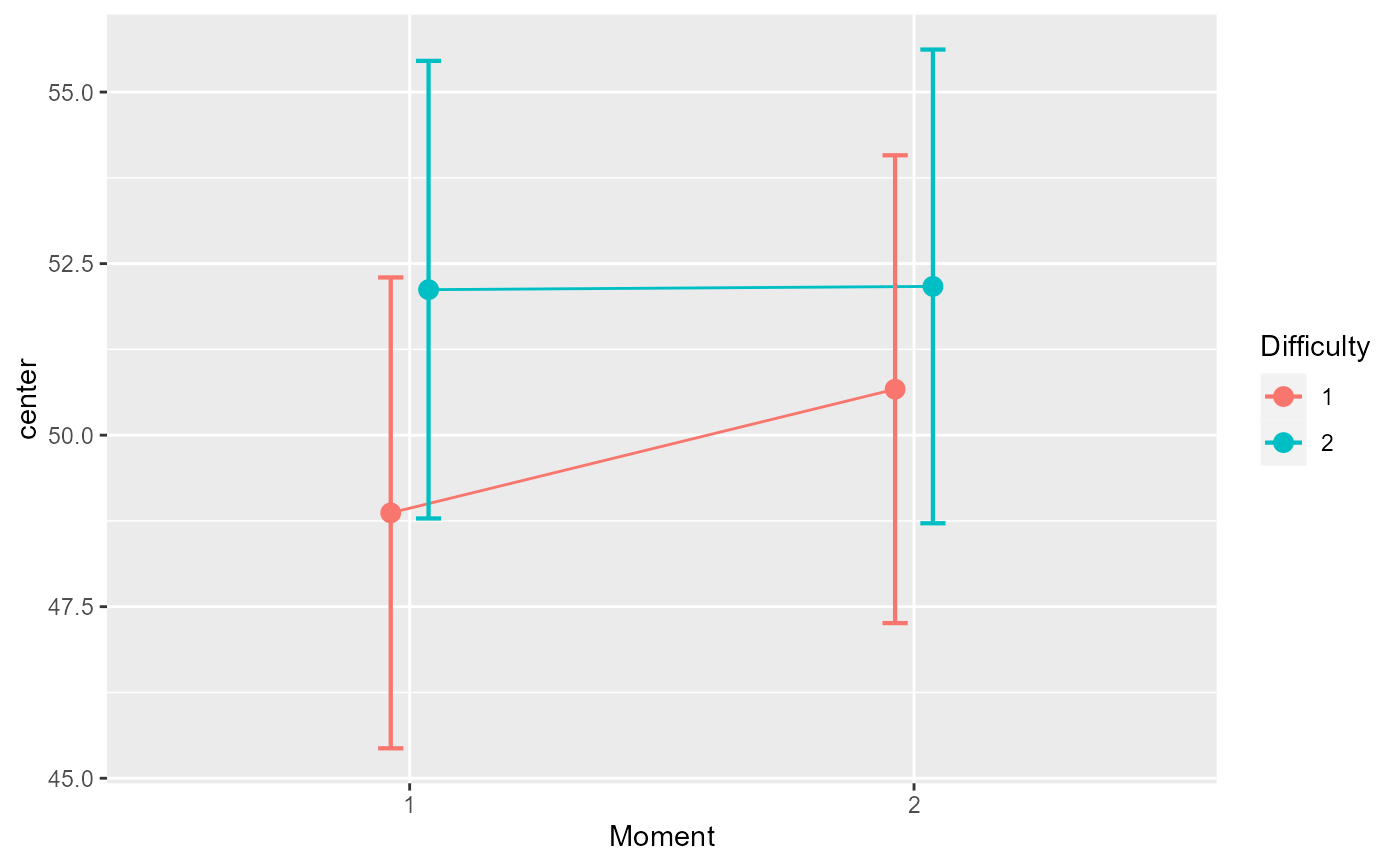# ... and the mean plot on the decorrelated data;
# because of high correlation, the error bars are markedly different
superb(cbind(DV.1,DV.2) ~ Difficulty, dta, WSFactors = "Moment(2)",
plotLayout="line",
adjustments = list (purpose="difference", decorrelation = "CM") )
# This example creates a dataset in a 3 x 2 design. It has various effects,
# one effect of difficulty, with an overall effect of 10 more (+3.33 per level),
# one effect of gender, whose slope is 10 points (+10 points for each additional gender),
# and finally one interacting effect, which is 0 for the last three cells of the design:
GRD(
SubjectsPerGroup = 10,
BSFactors = c("difficulty(3)","gender(2)"),
Population = list(mean=100,stddev=15),
Effects = list(
"difficulty" = extent(10),
"gender"=slope(10),
"difficulty*gender"=custom(-300,+200,-100,0,0,0)
)
)
#> id difficulty gender DV
#> 1 1 1 1 -195.342523
#> 2 2 1 1 -204.228477
#> 3 3 1 1 -213.830005
#> 4 4 1 1 -202.994646
#> 5 5 1 1 -216.461256
#> 6 6 1 1 -181.206409
#> 7 7 1 1 -221.245465
#> 8 8 1 1 -212.179467
#> 9 9 1 1 -238.964068
#> 10 10 1 1 -218.646576
#> 11 11 2 1 297.695425
#> 12 12 2 1 279.121187
#> 13 13 2 1 282.206213
#> 14 14 2 1 296.369687
#> 15 15 2 1 297.723655
#> 16 16 2 1 306.918428
#> 17 17 2 1 288.999651
#> 18 18 2 1 298.887454
#> 19 19 2 1 286.332888
#> 20 20 2 1 283.216963
#> 21 21 3 1 29.597093
#> 22 22 3 1 -9.606141
#> 23 23 3 1 -8.828696
#> 24 24 3 1 19.480856
#> 25 25 3 1 -5.177055
#> 26 26 3 1 -2.687536
#> 27 27 3 1 -9.482834
#> 28 28 3 1 -2.391428
#> 29 29 3 1 -2.371699
#> 30 30 3 1 -6.651541
#> 31 31 1 2 77.144242
#> 32 32 1 2 117.343487
#> 33 33 1 2 82.043130
#> 34 34 1 2 74.254958
#> 35 35 1 2 82.931952
#> 36 36 1 2 85.722843
#> 37 37 1 2 124.288892
#> 38 38 1 2 102.517204
#> 39 39 1 2 86.377333
#> 40 40 1 2 120.126938
#> 41 41 2 2 105.330652
#> 42 42 2 2 101.894918
#> 43 43 2 2 88.203652
#> 44 44 2 2 89.581522
#> 45 45 2 2 109.710517
#> 46 46 2 2 90.476951
#> 47 47 2 2 100.724557
#> 48 48 2 2 100.787167
#> 49 49 2 2 103.195492
#> 50 50 2 2 123.581083
#> 51 51 3 2 86.886100
#> 52 52 3 2 106.736054
#> 53 53 3 2 92.392109
#> 54 54 3 2 115.860219
#> 55 55 3 2 109.572412
#> 56 56 3 2 99.105086
#> 57 57 3 2 117.838338
#> 58 58 3 2 96.701243
#> 59 59 3 2 107.563433
#> 60 60 3 2 137.394063
# This last example creates a single group dataset,
# The instrument is assumed to return readings to
# plus or minus 0.1 only
GRD(
SubjectsPerGroup = 10,
Population = list(mean=100,stddev=15),
Instrument = list(
precision = 0.1
)
)
#> id DV
#> 1 1 102.5
#> 2 2 126.3
#> 3 3 80.6
#> 4 4 120.2
#> 5 5 117.7
#> 6 6 81.0
#> 7 7 76.4
#> 8 8 73.4
#> 9 9 115.4
#> 10 10 102.5